date�FSep. 30 2025 version�F1D
�r�W�l�X�����ϕ��ibusiness calculus�j
�r�W�l�X �����ϕ�
�����ϕ��̂����炢
�P�D�����ϕ��̗��j
�@�P�V���I�ɉ��B�Ŋm�����ꂽ�����ϕ��w�ɂ͏d�v�l�����Q�l�o�ꂵ�܂��B�C�M���X�̈̑�ȉȊw�҂ł������j���[�g���ƁA�h�C�c�̓N�w�҂ł��萔�w�҂ł����������C�v�j�b�c�ł��B�@�@�@�@�@�@�@�@�@
 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�j���[�g���i�p�F1643�`1727�F84�Ζv�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���C�v�j�b�c�i�ƁF1646�`1716�F70�Ζv�j
�@1704�N�F�j���[�g���w���Ϙ_�x�Ŕ����ϕ��̐��ʂ\�@�@�@�@�@1684�N�F���C�v�j�b�c�w�����ϕ��̘_���x���\
�@�ނ�͒��ǂ������ϕ��w��������̂ł͂���܂���B�ނ���ǂ��炩����ɔ����ϕ��w��n�n�������ɂ��āA�C�M���X�ƃh�C�c�̊w��������Ă��Ȃ范�������������ł����B�N��I�Ɍ����A�����ϕ��̊T�O�z�����̂̓j���[�g������ł������A�_���Ƃ��Č��\�����ɑ���o�����̂̓��C�v�j�b�c�̕�����ł����B���̂��߃C�M���X�̊w��́A���C�v�j�b�c�̓j���[�g���̖����\�_���𓐍삵���Ɣ��܂����B���R���C�v�j�b�c�����ق��Ă��炸�A���������̉��V�����N���̊Ԃɂ킽���đ������ƂɂȂ��Ă��܂��̂ł����A�ނ�̔����ϕ��w�̑g�ݗ��ĕ��͂��قȂ��Ă���A���݂ł͂Q�l�͓Ɨ��ɔ����ϕ��w���\�z�����ƍl�����Ă��܂��B
�@17���I�ɐ��������w��2�l�̓V�˂́A�j���[�g����84�Ζv�A���C�v�j�b�c��70�Ζv�Ɠ����Ƃ��Ă͐��ɒ����ł����B���̎���̉��y�E�ł́uG����̃A���A�v�̃o�b�n�i1685�N�`1750�N�j�������菭���O�̎���ł��B���{�ł́A����5�㏫�R�E����j�g�̌��\����ł���܂��B�����ł��A�����ϕ���300�N�ȏ�O�ɂł����g�ÓT�I���w�h�Ȃ̂ł��B
�Q�D����(differentiation)
�@�����𗝉�����O�ɋɌ��𗝉�����K�v������܂��B�Ɍ��Ƃ́h����Ȃ��Z�Z�ɋ߂Â��h���Ƃł��B1�����������{�P�́A����1�Ɍ���Ȃ��߂Â��A����2�Ɍ���Ȃ��߂Â��܂��B�����2�Ɏ�������Ƃ����A2���������{�P�̋Ɍ��l�Ƃ����܂��B�@�@�@�@�@�@�@�@
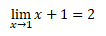
��y=f(x)�ɂ���x=a�̂Ƃ���y=��(a)�ŕ\�킵�܂��B�ϐ�x��a����b�܂ŕω�����Ƃ��Ay��f(a)����f(b)�܂ŕω����܂��B
������f(a+�����j-f(a)�@
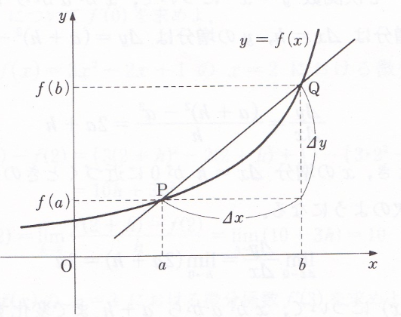

�@���ϕω�����
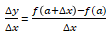 �ƂȂ�܂��B����������Ȃ�0�ɋ߂Â���A���ϕω��������̒l�Ɏ�������Ȃ�A���̋Ɍ��l����y=f(x)��x=a�ɂ���������W���idifferentialcoefficient�j�Ƃ����Af�f(a)�ŕ\�킵�܂��B
�ƂȂ�܂��B����������Ȃ�0�ɋ߂Â���A���ϕω��������̒l�Ɏ�������Ȃ�A���̋Ɍ��l����y=f(x)��x=a�ɂ���������W���idifferentialcoefficient�j�Ƃ����Af�f(a)�ŕ\�킵�܂��B�@�@�@�@f�f(a)=
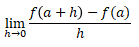
�@�����W����a�_�ł̕ω����ł����A������������i���j�ɂ��Ċ����f�i���j�����̓����iderived function�j�Ƃ����A���f�i���j�ŕ\�킵�܂��B���������߂邱�Ƃ��C�����Ƃ����܂��B
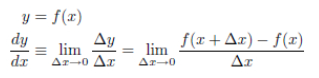
��x ���[���ɋ߂Â��ƁC������x�ɂ�����f(x)�̐ڐ��ɋ߂Â��܂��B�u���������߂�(�����j�v�Ƃ́C���̐ڐ��̎������߂邱�ƂȂ̂ł��B
�@�����̕\���ɂ́A�j���[�g���́A
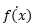 �A���C�v�j�b�c��
�A���C�v�j�b�c��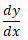 �A���O�����W����
�A���O�����W����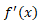 �Ƃ����悤�ɕ\�����܂����B����ł́A���C�v�j�b�c���ƃ��O�����W�������p�����Ă��܂��B
�Ƃ����悤�ɕ\�����܂����B����ł́A���C�v�j�b�c���ƃ��O�����W�������p�����Ă��܂��B�y�r�W�l�X�����ϕ��ŏd�v�Ȏ����z
�@�����ɂ��A���v/����/�R�X�g/cashflow���̍ő�l/�ŏ��l�����߂邱�Ƃ��ł��܂��B�l������Ă����Ԃň�ԑ傫���̂��ő�l�iglobal maximum,maximum value�j�A�����Ԃň�ԑ傫���̂��ɑ�l�ilocal maximum,maximul value�j�A�������̂����l�ɍŏ��l�iglobal minimum,minimum value�j�A�ɏ��l�ilocal minimum,minimul value�j�Ƃ����܂��B�ő�l�͋ɑ�l�ł����A�ɑ�l�͕K�������ő�l�ł͂���܂���B�ɑ�l�Ƌɏ��l���ɒl�Ƃ����܂����A����͓���f'(x)��0�ɂȂ�Ƃ���ł��Bf'(x)���{����-�Ȃ�ʂŋɑ�l�A-����{�Ȃ牚�ŋɏ��l�ɂȂ�܂��B
�@�Ⴆ�Ay=x^3-3x�̃O���t�͎��̂悤�ɂȂ�܂����A�ɏ��l��-2�ŋɑ�l��+2�ɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@
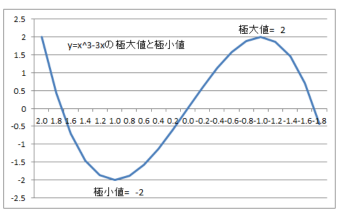
2�����������ł͋ɒl�ƍő�l�E�ŏ��l����v���܂��̂ŁA��������������0�Ƃ��Ă������߂�A�ő�l�E�ŏ��l�����܂�܂��B
�y�d�v�Ȕ��������z
�@�@
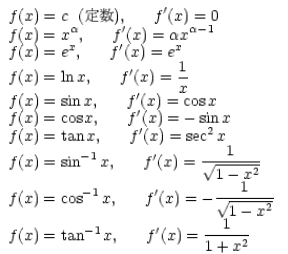 �@�@�@�@�@
�@�@�@�@�@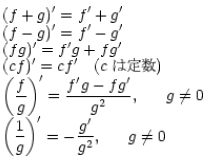 �@�@�@�@�@
�@�@�@�@�@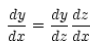
�@�@�@
�R�D�ϕ��iintegral�j
�@�ϕ��͑傫��2�ɕ������܂��B�i1�j��ϕ��idefinite integral�j
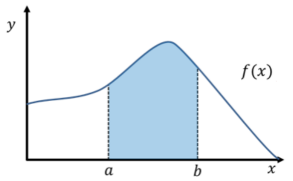
�@��ϕ��Ƃ́A���W���ʏ�Ɋ����`���O���t�ƍ��W���Ɉ͂܂ꂽ���̕����̖ʐς����߂���@�������܂��B�ǂ�Ȃɕ��G�Ȍ`��̐}�`�ł��C�ׂ����X���C�X����C�����`�̒Z���̏W���ɒu�������邱�Ƃ��ł��܂��B�Z���̖ʐς́u�X���C�X���~�Z���̍����v�ł��B�Z���̖ʐς����ׂč��v����C�}�`�̖ʐςƂقړ������Ȃ�܂��B���ꂪ��ϕ��̌����ł��B�}�`�̌`���\������ f(x) �C�}�`���X���C�X���镝�� dx �Ƃ���ƁC�}�`�̖ʐς͎��̎��œ����܂��B
 �@�@�@
�@�@�@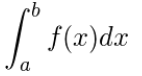
�@�ϕ��̎�����dx�́A���ɏ����Ȓ�����\���Ă��܂��B�܂��Af(x)dx�́A���i���j��dx�̐ς�\���Ă��܂��B���i���j�͂���_���ɂ������f�i���j�l�ł��邱�Ƃ���Aa-b�Ԃ���ɍׂ������������`�̏W���Ƃ����܂��Ba-b�Ԃ��Ɍ��܂ōׂ�������A���i���j��a-b�Ԃ̖ʐς����߂��܂��B���̂悤�ɁC�O���t��̂��镔���̖ʐς��C��̓I�Ȑ��l���邢�͕ϐ��Ŏ������@����ϕ��ł��B
�i2�j�s��ϕ��iindefinite integral�j
�@����1�́C�����̋t�̉��Z�Ŕ�������O�̊������߂���@�ł��B�����s��ϕ��A���邢�͌��n���iprimitive function�j�����߂�Ƃ����܂��B
���̗�ł́C�萔�����܂ގ��̔���������ƁC�萔������������܂��B���̂��Ƃ���C�����̋t���Z�ł���ϕ����s���ƁC�萔�����\���͂��ł��B
�@�@�@�@�@�@�@�@�@�@�@�@
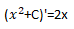 ����
�����@�@�@�@�@�@
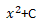 �@�@�@�@���|�|�|���@�@�@
�@�@�@�@���|�|�|���@�@�@�@�@�@�@�@�@�@�@�@�@�@
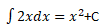 �@�ϕ�
�@�ϕ��@���̒萔�� C ��ϕ��萔�iintegration constant�j�Ƃ����܂��B�P���ɐϕ����������ł́C���̐ϕ��萔������ł��܂���B���肳��Ȃ��Ԃ́C�ϕ��萔��萔�L�� C �ŕ\���܂��B
�y�r�W�l�X�����ϕ��ŏd�v�Ȏ����z
�@�ʐς����߂��ϕ������p����܂��B�����ł́A���G�Ȍv�Z�ɂȂ�܂��̂Ŏ��Ɖ��M�ł͎d���ɂȂ�܂���B�r�W�l�X�f�[�^�̐������̕łɂ���Excel VBA�x�[�X�́u�V���v�\�������ɂ���ϕ��̌v�Z�v�A�v�����g�p���܂��B
�@�@
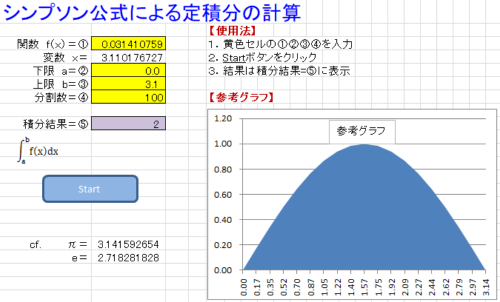
�y�d�v�Ȑϕ������z
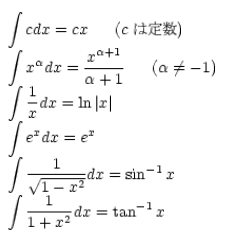 �@�@�@�@�@
�@�@�@�@�@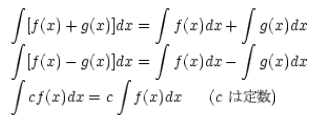 �@�@�@
�@�@�@